# 理解递归

要理解递归，首先要理解递归。

递归是一种解决问题的方法，它从解决问题的各个小部分开始，直到解决最初的大问题。递归通常涉及函数调用自身。每个递归函数都必须有基线条件,即一个不再递归调用的条件（停止点）,以防止无限递归。

# 计算一个数的阶乘

 function factorial(number) {
    console.trace()
    if (number === 1) {
        return 1
    }
    return number * factorial(number - 1)
}

每当一个函数被一个算法调用时，该函数会进入调用栈的顶部。当使用递归的时候，每个函数调用都会堆叠在调用栈的顶部，这是因为每个调用都可能依赖前一个调用的结果

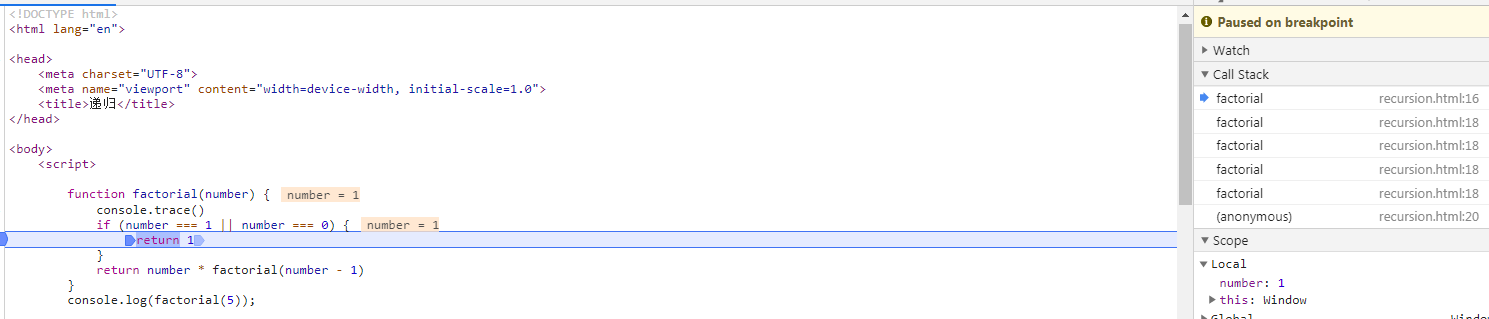
打开浏览器的开发者工具，打开 Sources 标签页，在 Factorial.js文件中增加一个断点，当 n 的值为 1 时，我们可以看到 Call Stack 里有三个 factorial 函数的调用。如果继续执行，会看到当 factorial(1)被返回后，Call Stack 开始弹出 factorial 的调用

# JavaScript 调用栈大小的限制

如果忘记加上用以停止函数递归调用的基线条件，会发生什么呢？递归并不会无限地执行下去，浏览器会抛出错误，也就是所谓的栈溢出错误（stack overflow error）。

    let i = 0;
    function recursiveFn() {
        i++;
        recursiveFn();
    }
    try {
        recursiveFn();
    } catch (ex) {
        console.log('i = ' + i + ' error: ' + ex);
    }

15719 error: RangeError: Maximum call stack size exceeded 在本地电脑 Chrome 中，该函数执行了 15719 次浏览器抛出错误

# 递归优化

函数调用自身,成为递归. 如果尾调用自身,就称为尾递归. 递归需要保存大量的调用记录,很容易发生栈溢出错误,如果使用尾递归优化,将递归变为循环,那么只需要保存一个调用记录,这样就不会发生栈溢出错误了。

因此上面的阶乘我们可以改成下面这样

function factorial(number, total) {
    if (number === 1) {
        return total
    }
    return factorial(number - 1, number * total)
}

factorial(5, 1)

再次查看 Call Stack 发现还是那么多执行栈,并没有减少,这是为什么呢?

function runStack(n) {
    if (n === 0) return 100
    return runStack(n - 2)
}

runStack(20000)

// 改成while
function runStack(n) {
    while (true) {
        if (n === 0) {
            return 100
        }
        if (n === 1) {
            return 200
        }
        n = n - 2
    }
}

蹦床函数

function runStack(n) {
    if (n === 0) return 100
    return runStack.bind(null, n - 2)
}

function trampoline(f) {
    while (f && f instanceof Function) {
        f = f()
    }
    return f
}
trampoline(runStack(100000))

前面我们已经使用了尾递归优化可还是爆栈了,因为浏览器不支持. 但是改成 while 和 蹦床函数后发现没任何问题

# 斐波那契数列

斐波那契数列是另一个可以用递归解决的问题。它是一个由 0、1、1、2、3、5、8、13、21、34 等数组成的序列。数 2 由 1 + 1 得到，数 3 由 1 + 2 得到，数 5 由 2 + 3 得到，

位置0的斐波那契数是0
1 和 2 的斐波那契数是 1。
n（此处 n > 2）的斐波那契数是（n  1）的斐波那契数加上（n  2）的斐波那契数。

function fibonacci(n){ 
 if (n < 1) return 0; // {1} 
 if (n <= 2) return 1; // {2} 
 return fibonacci(n - 1) + fibonacci(n - 2); // {3} 
}

实现栈 →