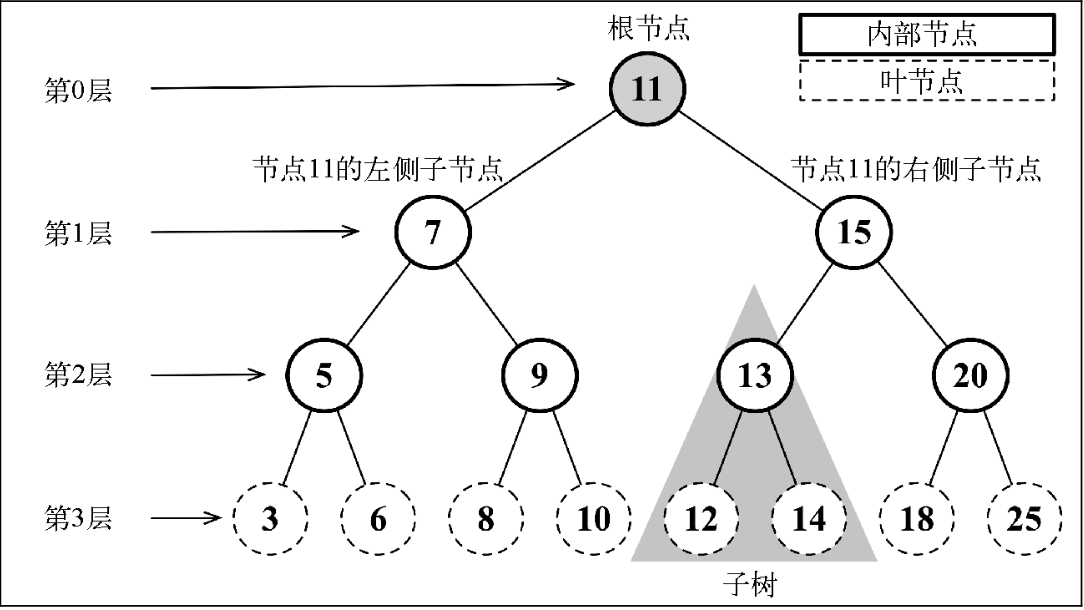
# 树的相关术语

一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点(除了顶部的第一个节点)以及零个或多个子节点:

tree

每个节点可以用以下数据结构来表示：

Node {
	value: any; // 当前节点的值
	children: Array<Node>; // 指向其儿子
}

其他重要概念：

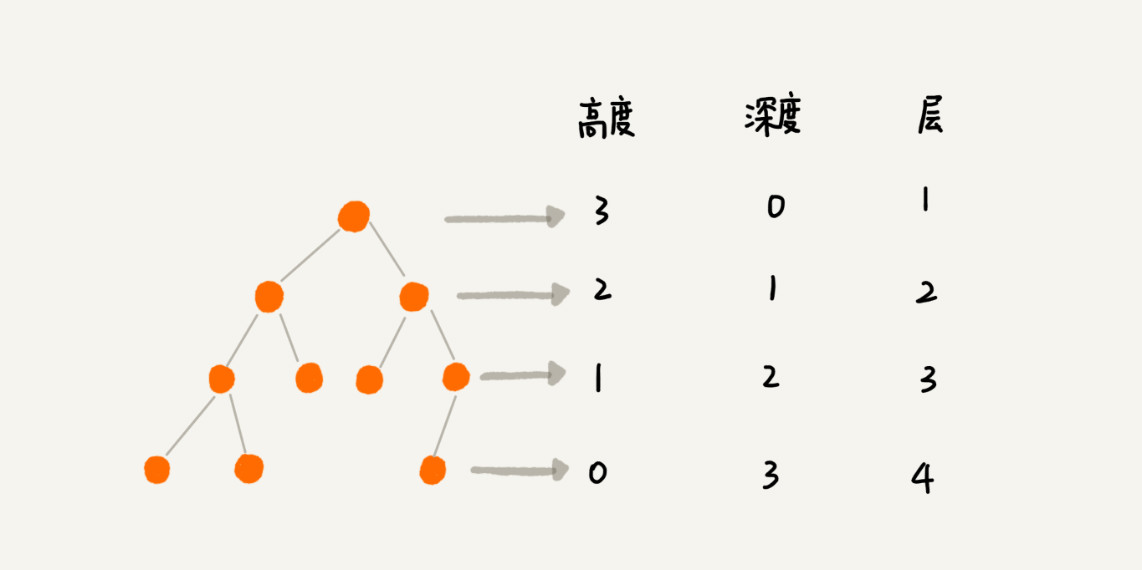
树的高度、树的深度、树的层、二叉树，三叉树，。。。 N 叉树

tree

# 二叉树和二叉搜索树

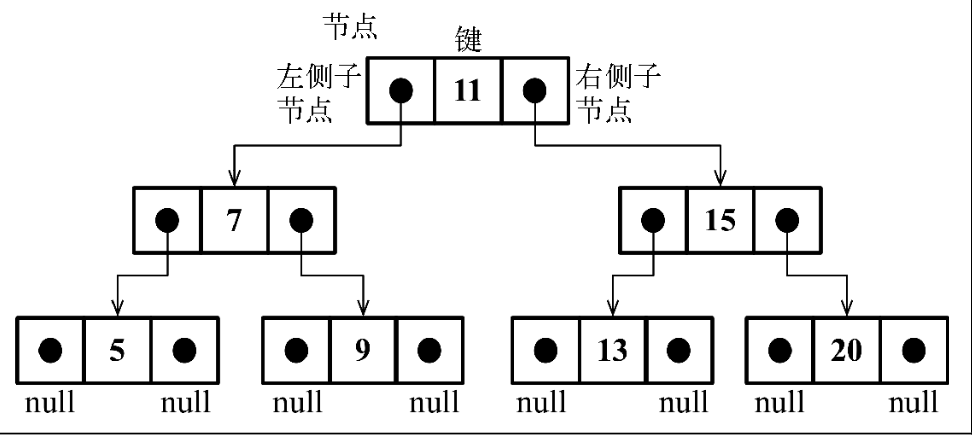
二叉树 中的节点最多只能有两个子节点:一个是左侧子节点，另一个是右侧子节点。

二叉搜索树(BST) 是二叉树的一种，但是只允许你在左侧节点存储(比父节点) 小的值，在右侧节点存储(比父节点) 大的值

下图展现了二叉搜索树数据结构的组织方式。

tree

# 实现二叉搜索树

下面是将要在 BinarySearchTree 类中实现的方法：

insert(key):向树中插入一个新的键。
search(key):在树中查找一个键。如果节点存在，则返回 true;如果不存在，则返回 false。
inOrderTraverse():通过中序遍历方式遍历所有节点。
preOrderTraverse():通过先序遍历方式遍历所有节点。
postOrderTraverse():通过后序遍历方式遍历所有节点。
min():返回树中最小的值/键。
max():返回树中最大的值/键。
remove(key):从树中移除某个键。

实现

class Node {
    constructor(key) {
        this.key = key
        this.left = null
        this.right = null
    }
}

const Compare = {
    LESS_THAN: '<',
    BIGGER_THAN: '>'
}

const defaultCompare = (a, b) => a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN


class BinarySearchTree {
    constructor(compareFn = defaultCompare) {
        this.compareFn = compareFn
        this.root = null
    }

    /**
     * 向树中插入一个新的键
     * @param {*} key 
     */
    insert(key) {
        if (this.root == null) {
            this.root = new Node(key)
        } else {
            this.insertNode(this.root, key)
        }
    }

    insertNode(node, key) {
        if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
            if (node.left == null) {
                node.left = new Node(key)
            } else {
                this.insertNode(node.left, key)
            }
        } else {
            if (node.right == null) {
                node.right = new Node(key)
            } else {
                this.insertNode(node.right, key)
            }
        }
    }

    /**
     * 在树中查找一个键。如果节点存在，则返回 true；如果不存在，则返回false。
     * @param {*} key 
     */
    search(key) {
        return this.searchNode(this.root, key)
    }

    searchNode(node, key) {
        if (node == null) {
            return false
        }
        if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
            return this.searchNode(node.left, key);
        } else if (
            this.compareFn(key, node.key) === Compare.BIGGER_THAN
        ) {
            return this.searchNode(node.right, key);
        } else {
            return true;
        }
    }

    /**
     * 通过中序遍历方式遍历所有节点
     */
    inOrderTraverse(callback) {
        this.inOrderTraverseNode(this.root, callback)
    }

    inOrderTraverseNode(node, callback) {
        if (node != null) {
            this.inOrderTraverseNode(node.left, callback)
            callback(node.key)
            this.inOrderTraverseNode(node.right, callback)
        }
    }

    /**
     * 通过先序遍历方式遍历所有节点
     */
    preOrderTraverse() {
        this.preOrderTraverseNode(this.root, callback)
    }

    preOrderTraverseNode(node, callback) {
        if (node != null) {
            callback(node.key)
            this.preOrderTraverseNode(node.left, callback)
            this.preOrderTraverseNode(node.right, callback)
        }
    }

    /**
     * 通过后序遍历方式遍历所有节点。
     */
    postOrderTraverse(callback) {
        this.postOrderTraverseNode(this.root, callback)
    }

    postOrderTraverseNode(node, callback) {
        if (node != null) {
            this.postOrderTraverseNode(node.left, callback)
            this.postOrderTraverseNode(node.right, callback)
            callback(node.key)
        }
    }

    /**
     * 返回树中最小的值/键。
     */
    min() {
        return this.minNode(this.root)
    }

    minNode(node) {
        let current = node
        while (current != null && current.left != null) {
            current = current.left
        }
        return current
    }

    /**
     * 返回树中最大的值/键。
     */
    max() {
        return this.maxNode(this.root)
    }

    maxNode(node) {
        let current = node
        while (current != null && current.right != null) {
            current = current.right
        }
        return current
    }

    /**
     * 从树中移除某个键
     * @param {*} key 
     */
    remove(key) {
        this.root = this.removeNode(this.root, key)
    }

    removeNode(node, key) {
        if (node == null) {
            return null
        }
        if (this.compareFn(key, node.key) === Compare.LESS_THAN) { // {3} 
            node.left = this.removeNode(node.left, key); // {4} 
            return node; // {5} 
        } else if (
            this.compareFn(key, node.key) === Compare.BIGGER_THAN
        ) { // {6} 
            node.right = this.removeNode(node.right, key); // {7} 
            return node; // {8} 
        } else {
            // 键等于 node.key 
            // 第一种情况
            if (node.left == null && node.right == null) { // {9} 
                node = null; // {10} 
                return node; // {11} 
            }
            // 第二种情况
            if (node.left == null) { // {12} 
                node = node.right; // {13} 
                return node; // {14} 
            } else if (node.right == null) { // {15} 
                node = node.left; // {16} 
                return node; // {17} 
            }
            // 第三种情况
            const aux = this.minNode(node.right); // {18} 
            node.key = aux.key; // {19} 
            node.right = this.removeNode(node.right, aux.key); // {20} 
            return node; // {21} 
        }
    }
}

# 自平衡树

AVL 树是一种自平衡二叉搜索树，意思是任何一个节点左右两侧子树的高度之差最多为 1

AVL 树是一个 BST，我们可以扩展我们写的 BST 类，只需要覆盖用来维持 AVL 树平衡的方法，也就是 insert、insertNode 和 removeNode 方法。所有其他的 BST 方法将会被 AVLTree 类继承。

平衡操作-AVL旋转

在对 AVL 树添加或移除节点后，我们要计算节点的高度并验证树是否需要进行平衡。向 AVL 树插入节点时，可以执行单旋转或双旋转两种平衡操作，分别对应四种场景。

左-左(LL):向右的单旋转
右-右(RR):向左的单旋转
左-右(LR):向右的双旋转(先 LL 旋转，再 RR 旋转)
右-左(RL):向左的双旋转(先 RR 旋转，再 LL 旋转)

# 红黑树

和 AVL 树一样，红黑树也是一个自平衡二叉搜索树，在红黑树中，每个节点都遵循以下规则:

顾名思义，每个节点不是红的就是黑的;
树的根节点是黑的;
所有叶节点都是黑的(用 NULL 引用表示的节点);
如果一个节点是红的，那么它的两个子节点都是黑的;
不能有两个相邻的红节点，一个红节点不能有红的父节点或子节点;
从给定的节点到它的后代节点(NULL 叶节点)的所有路径包含相同数量的黑色节点。

← LUR 算法实现解题套路 →