# 解题套路
# 二叉树遍历
二叉树的大部分题都围绕二叉树遍历展开,二叉树主要有以下遍历方式:
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历(BFS)
# 前序遍历
前序遍历的顺序
- 访问当前节点
- 遍历左子树
- 遍历右子树
如下动图很好地演示了前序遍历算法的过程。
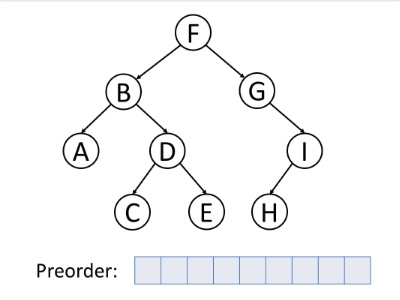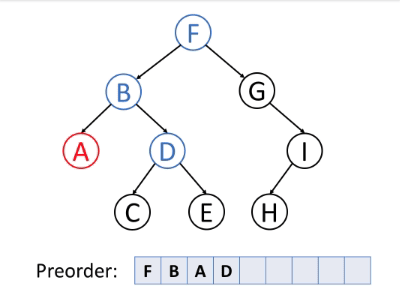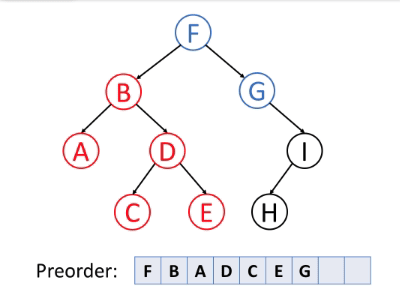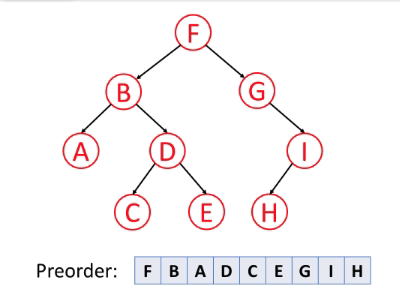
前序遍历的伪代码
preorder(root) {
if not root: return
doSomething(root)
preorder(root.left)
preorder(root.right)
}
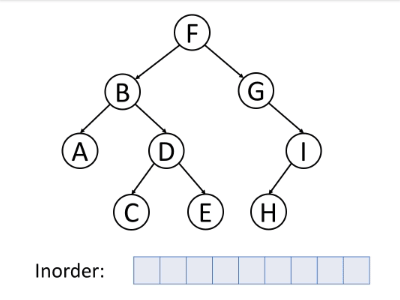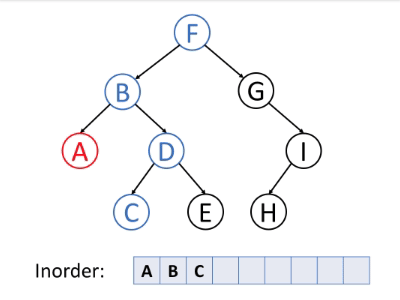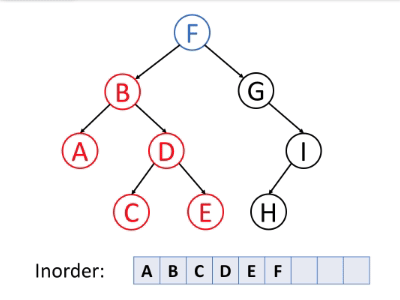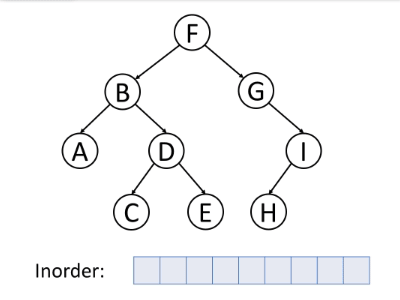
# 中序遍历
中序遍历的顺序
- 遍历左子树
- 访问当前节点
- 遍历右子树
如下动图很好地演示了中序遍历算法的过程。
中序遍历的伪代码
preorder(root) {
if not root: return
preorder(root.left)
doSomething(root)
preorder(root.right)
}
# 后序遍历
后序遍历的顺序
- 遍历左子树
- 遍历右子树
- 访问当前节点
如下动图很好地演示了后序遍历算法的过程。
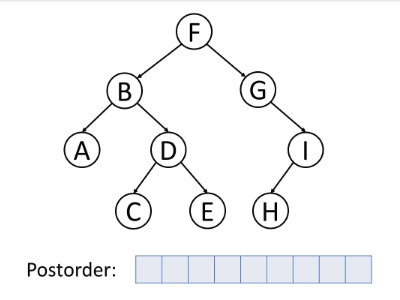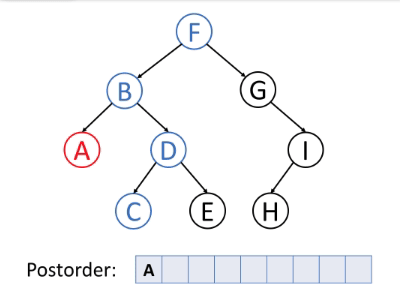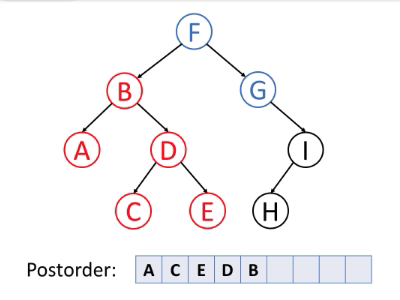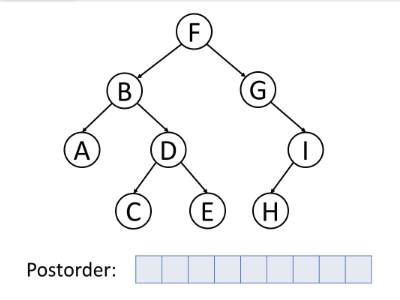
后序遍历的伪代码
preorder(root) {
if not root: return
preorder(root.left)
preorder(root.right)
doSomething(root)
}
# 层序遍历(BFS)
层次遍历从直观上会先遍历树的第一层, 再遍历树的第二层,以此类推,更多的时候还是使用借助队列的先进先出的特性来实现。
如下动图很好地演示了层序遍历算法的过程。
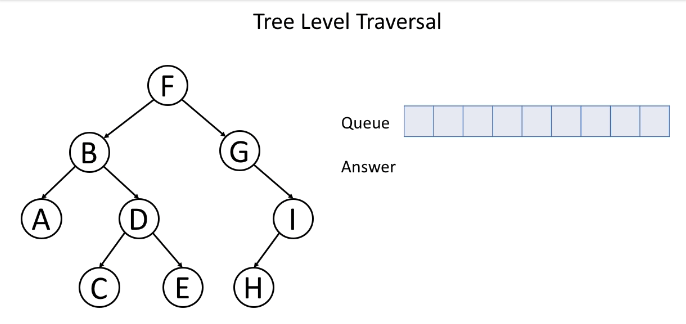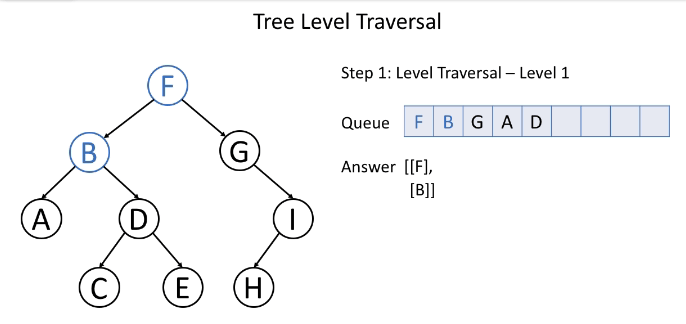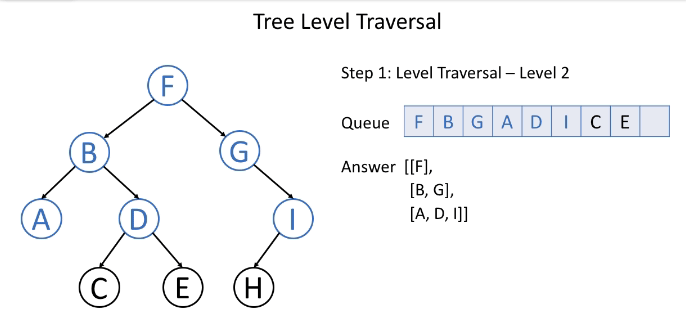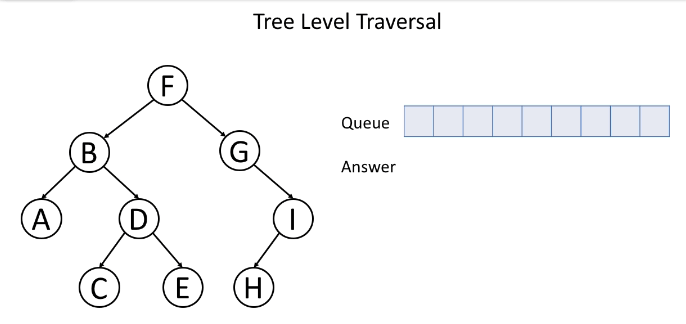
二叉树层次遍历伪代码:
bfs(root) {
queue = []
queue.push(root)
while queue.length {
curLevel = queue
queue = []
for i = 0 to curLevel.length {
doSomething(curLevel[i])
if (curLevel[i].left) {
queue.push(curLevel[i].left)
}
if (curLevel[i].right) {
queue.push(curLevel[i].right)
}
}
}
}
# 二叉树构建
从前序与中序遍历序列构造二叉树
题目描述
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
伪代码:
var buildTree = function(preorder, inorder) {
if(!inorder.length) return null
let tmp = preorder.shift(),mid = inorder.indexOf(tmp)
let root = new TreeNode(tmp)
root.left = buildTree(inorder.slice(0,mid))
root.right = buildTree(inorder.slice(mid+1))
return root
};
106. 从中序与后序遍历序列构造二叉树
889. 根据前序和后序遍历构造二叉树
226-116-114-654-105-106-889-652
套路类似
# 二叉搜索树
二叉搜索树是二叉树的一种,在前面已经说过、具有以下性质
- 左子树的所有节点值小于根的节点值(注意不含等号)
- 右子树的所有节点值大于根的节点值(注意不含等号)
由于二叉树的中序遍历是一个有序列表,我们可以有以下思路
- 对先序遍历结果排序,排序结果是中序遍历结果
- 根据先序遍历和中序遍历确定一棵树
230-538-1038-450-701-700-98-98-95
# 题目推荐
- 266翻转二叉树
- 114 二叉树展开为链表
- 116填充每个节点的下一个右侧节点指针(中等)
- 589N 叉树的前序遍历
- 662二叉树最大宽度 (请分别使用 BFS 和 DFS 解决,空间复杂度尽可能低)
- 834树中距离之和
- 967连续差相同的数字 (隐形树的遍历)
- 1145二叉树着色游戏(树上进行决策)
- lowest-common-ancestor-of-a-binary-tree
- binary-tree-level-order-traversal
- binary-tree-zigzag-level-order-traversal
- validate-binary-search-tree
- maximum-depth-of-binary-tree
- balanced-binary-tree
- binary-tree-level-order-traversal-ii
- binary-tree-maximum-path-sum
- insert-into-a-binary-search-tree